Two years ago we wrote a blogpost about the basic of basics within electronic theory: Voltage, Current and Resistance. Now we feel it’s time to pick the topic up again by introducing you to Kirchhoff’s Laws.
Quick Intro
Not only are Kirchhoff’s Laws good tools for analyzing and designing specific circuits. They are all also fundamental laws which give you an understanding of how electricity and physics work in general. So, even though you won’t use these laws as mathematical tools, you should know these principles by heart. And trust us: they are very simple and trivial!
The term Kirchhoff’s Laws encompasses two seperate laws:
- Kirchhoff’s Current Law aka. KCL
- Kirchhoff’s Voltage Law aka. KVL
We will go through these two laws one by one, but first we will explain two important terms related to these laws.
Nodes and Closed Paths
It’s important that you know what nodes and closed paths mean before moving on.
Nodes
A node is a point in a circuit where two or more circuit elements meet. These nodes are often junctions, but can also be just a point between two components. Nodes are important in KCL.
Closed Paths
A closed path aka. a loop is a path in a circuit from a node through a selection of circuit elements and back to the starting node without passing any other node more than once. A fiddly explanation, but it will all make sense in the image below.
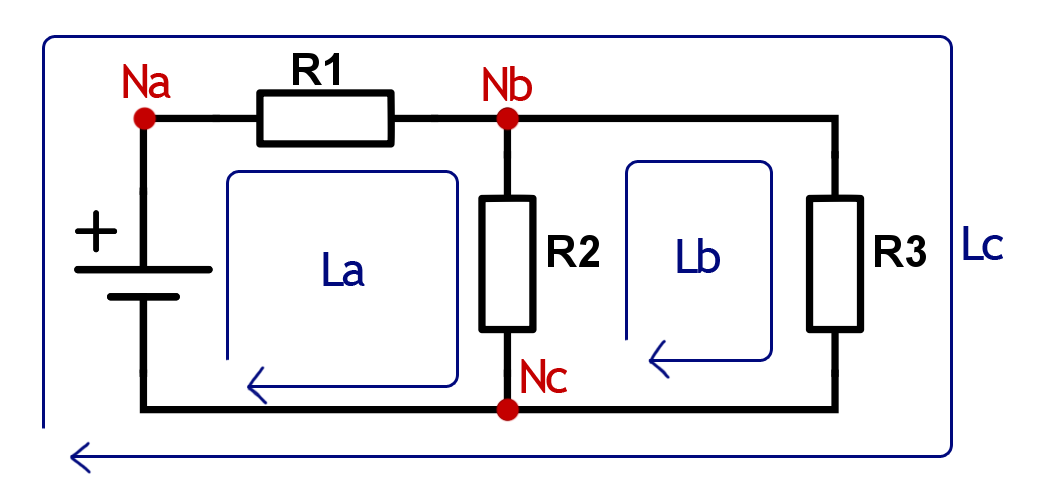
The direction you define for the path is important with regards to the mathematical operations in KVL. It doesn’t have to be the same direction as the current actually flows, but you must define a virtual direction nonetheless.
Kirchhoff’s Current Law (KCL)
KCL reads as follows:
The algebraic sum of all the currents at any node in a circuit equals zero.
This means that the current entering a node is always equal to the current exiting a node.
A node can have any number of “inputs” and any number of “outputs”. In the example above, Na has one input and one output. Nb has one input and two outputs. Nc has two inputs and one output.
NOTE: We don’t actually operate with inputs and outputs in KCL since we don’t always know which way the current flows. Instead we define positive directions for currents around a node. They don’t have to be physically correct, but they need to be defined. We then solve the equations, and if the result is positive, the current direction is equal to the direction we defined as positive, and vice versa.
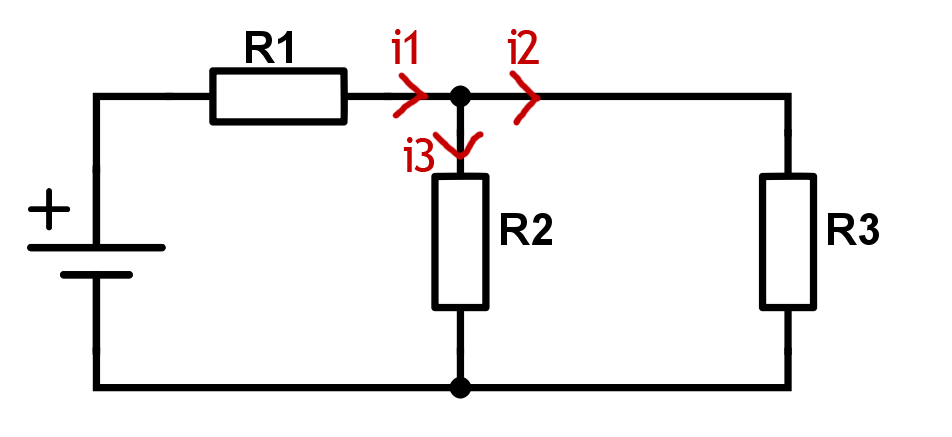In the image above we see a trivial example where
i1 = i2 + i3
or the equivalent
i1 – i2 – i3 = 0
for that node in the top center which we called Nb before. The currents’ signs (positive or negative) in these equations are like they are only because we have defined the directions in the drawing above as we have.
Kirchhoff’s Voltage Law (KVL)
The algebraic sum of all the voltages around any closed path in a circuit equals zero.
In other words: the sum of applied voltages around a closed path is equal to the sum of voltage drops around that closed path.
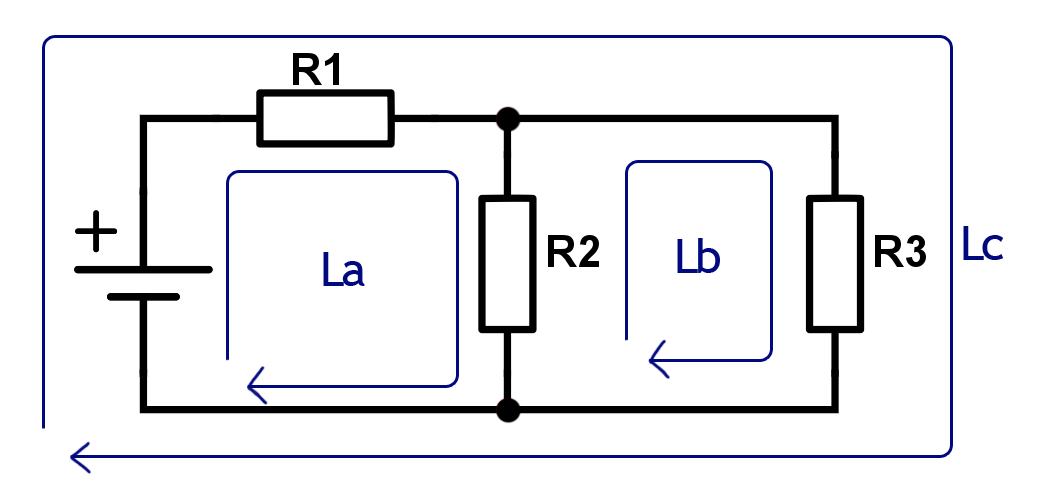Let’s look at this example and let’s call the voltage source E1. Let’s call the voltage drops over R1, R2 and R3 Vr1, Vr2 and Vr3.
Around the Lc path we get
E1 = Vr1 + Vr3
or
E1 – Vr1 – Vr3 = 0.
Additional Voltage Sources
If we insert another voltage source E2 somewhere along Lc with the opposite polarity of E1, we get
E1 – Vr1 – Vr3 – E2 = 0.
E2 is in this case counted as a voltage drop since we’ve defined a clockwise direction for Lc.
Going Further
You might wonder what’s the big whoop about these laws?
Well, firstly they are fundamental principles for all electricity. Secondly, KCL and KVL together with Ohm’s Law can be applied to analyze DC circuits and the combination of these can be quite powerful. This is something we’ll look at in a later post.
